Ebedi geometri sorusu: bir üçgenin alanı nasıl hesaplanır?

Matematikte en sık kullanılan rakamlardan biri. üçgenİlk bakışta, bu üç tarafı olan basit bir figür gibi görünebilir. Öte yandan, üçgen soruların sizi nasıl zorlayabileceğini görmek için üniversite giriş sınavlarındaki geometri sorularına bakmanız yeterli.

Sınırlı zamanı olan öğrenciler için zor üçgen sorularında okul sıralarını görüntüleyin ve açıların birbiriyle nasıl ilişkili olduğunu görün. son seviye patron etkileyebilir. Peki bu üçgenin alanı nasıl hesaplanır?

Alanı hesaplamak için kullanılan yöntemler üçgenin şekline göre farklılık gösterir. Bazen senin köşelerin alan kullanılarak bulunur alan bul İçin yükseklik bilmeniz yeterli olacaktır.

Bir üçgenin alanı nasıl hesaplanır?

• Taban ve yükseklik ile hesaplama
• Kenar uzunlukları ile hesaplama
• Eşkenar üçgenin bir tarafını kullanarak hesaplama
• Trigonometri ile hesaplama

Taban ve yükseklik ile hesaplama:

• Aşama 1: Üçgenin yüksekliği 3 cm olsun.
• Adım 2: Üçgenin taban genişliği 5 cm olsun.
• Aşama 3: Bu durumda formülümüz 1/2 x (taban yüksekliği x genişliği) olacaktır.
• Adım #4: 1/2 x (5×3)
• Adım 5: A = 1/2 x 15 cm
• Adım #6: Üçgen alan= 7,5 cm2

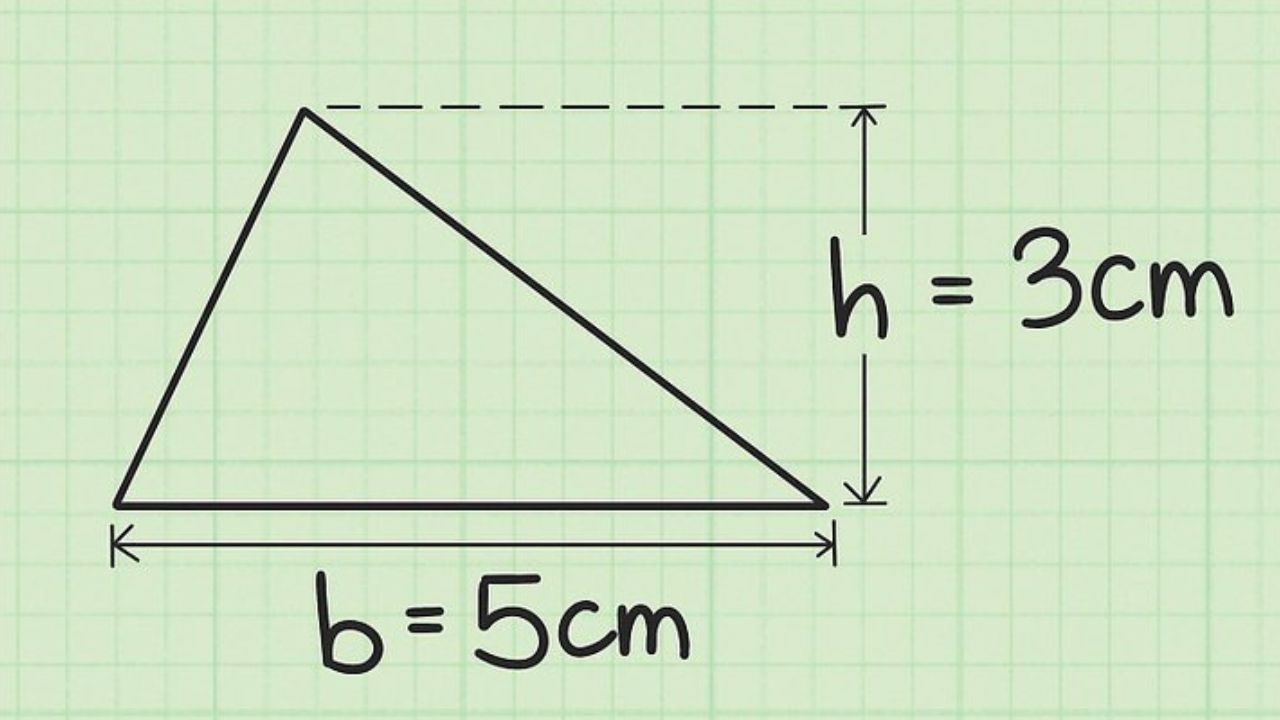
Bu yöntem en basit üçgen problemlerini çözmek için kullanılır. Yükseklik ve taban genişliği Bir kez öğrendikten sonra, yukarıdaki adımları izleyerek bir üçgenin alanını kolayca bulabilirsiniz.

Kenar uzunlukları ile hesaplama:

• Aşama 1: Önce kenarların uzunluklarını belirleyin. Bu örnekte kenar uzunlukları 3-4-5 cm olarak tanımlanmıştır.
• Adım 2: Bu durumda 1/2(a+b+c) formülünü kullanmalıyız.
• Aşama 3: 1/2(3+4+5)
• Adım #4: A: 1/2 x 12 cm
• Adım 5: Bir üçgenin alanı: 6cm2

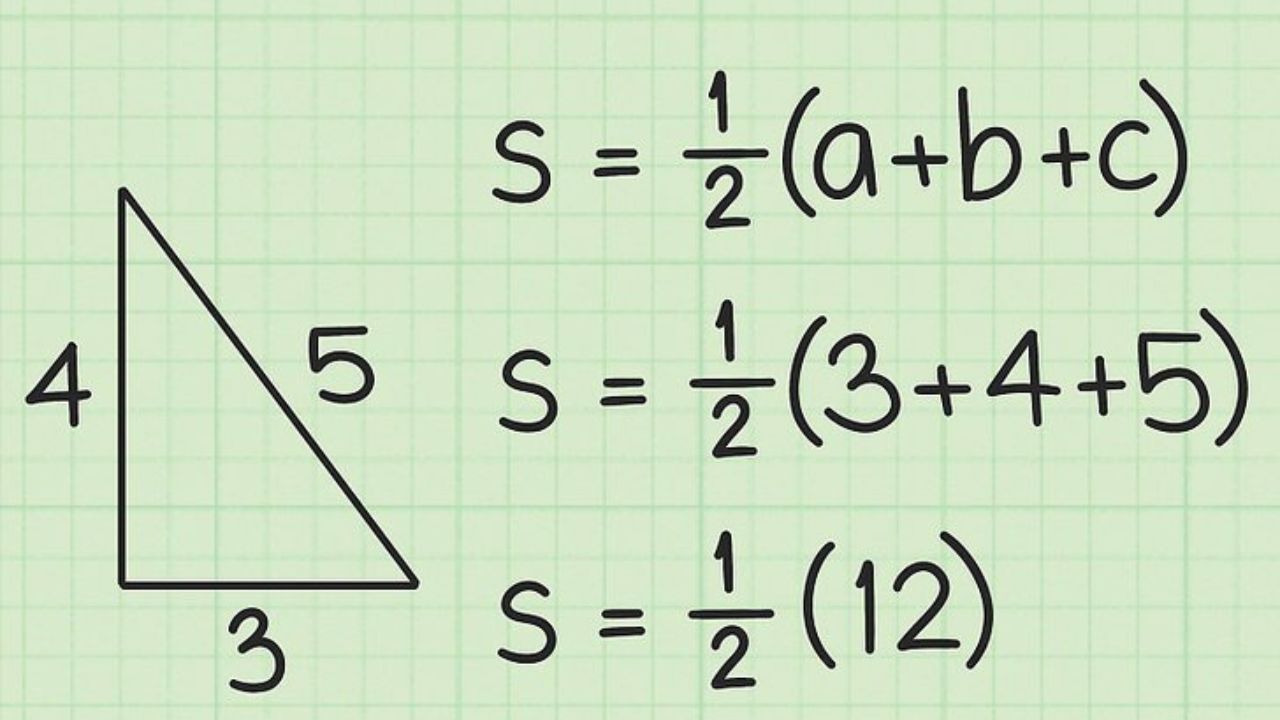
Bir üçgenin 3 kenarının uzunluklarını biliyorsanız, üçgenin alanını bulmak için önce çevresini bulup sonra 2’ye bölerek alanı hesaplayabilirsiniz. Bu yöntemlerin çoğu farklı varyasyonlar Ancak mantık, üç köşenin uzunluğunu toplayıp 2’ye bölmektir.

Eşkenar üçgenin bir tarafını kullanarak hesaplama:

• Aşama 1: Kenarlarımız 6 cm olsun.
• Adım 2: Bu yöntemde uzunluğun karesini alıp √3 ile çarpar ve 4’e böleriz.
• Aşama 3: A: 6×6 x √3/4
• Adım #4: A: 36 x √3/4
• Adım 5: Bir üçgenin alanı: 15.59 cm2

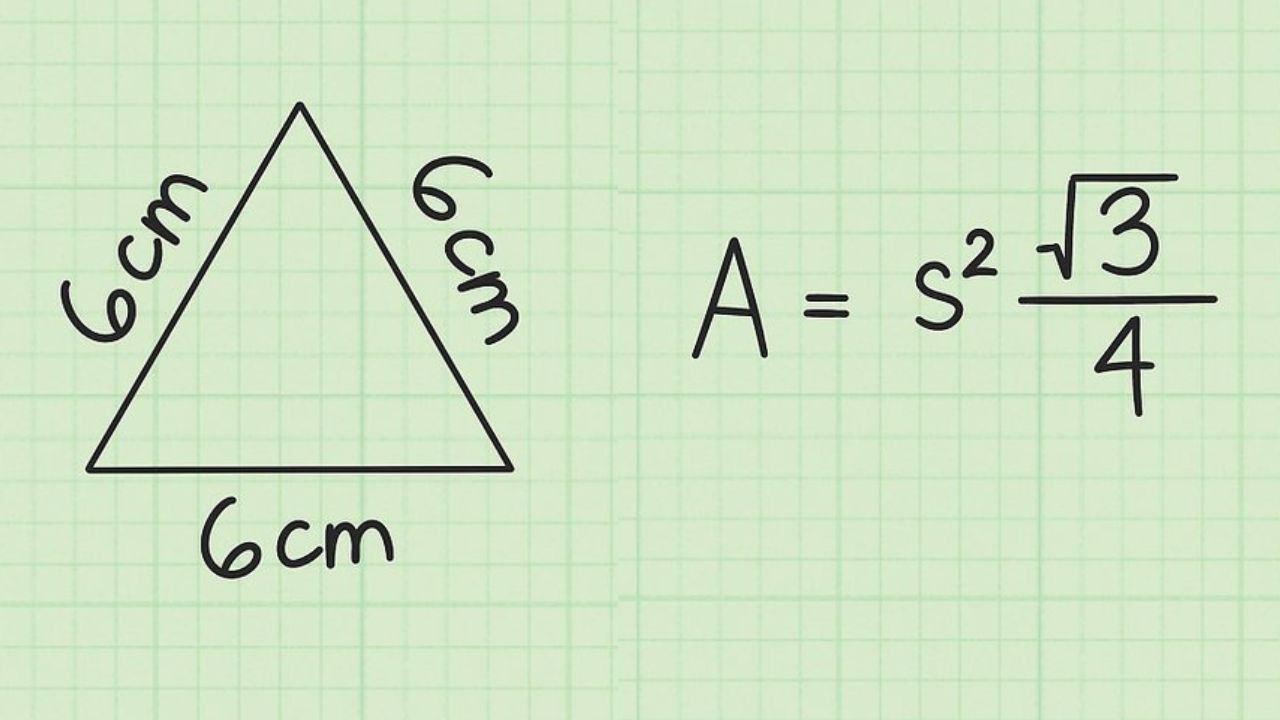
Eşit uzunlukta bir üçgeniniz varsa bir üçgenin alanını bulmak için bir kaburga yeterli olacaktır. Yukarıdaki adımları takip ederek uzunluğu bir formüle yazdığınızda matematik işlemlerini sırayla yaparak alanı kolayca bulabilirsiniz.

Trigonometri kullanarak hesaplama:

• Aşama 1: Önce 2 köşe uzunluğu ve 1 açı bulun.
• Adım 2: ab/2 x sinA formülünü uygulayın.
• Aşama 3: A: 150×231/2xsin123
• Adım #4: A: 17325X 0..83867 (sin123)
• Adım 5: Bir üçgenin alanı:14.530 cm2

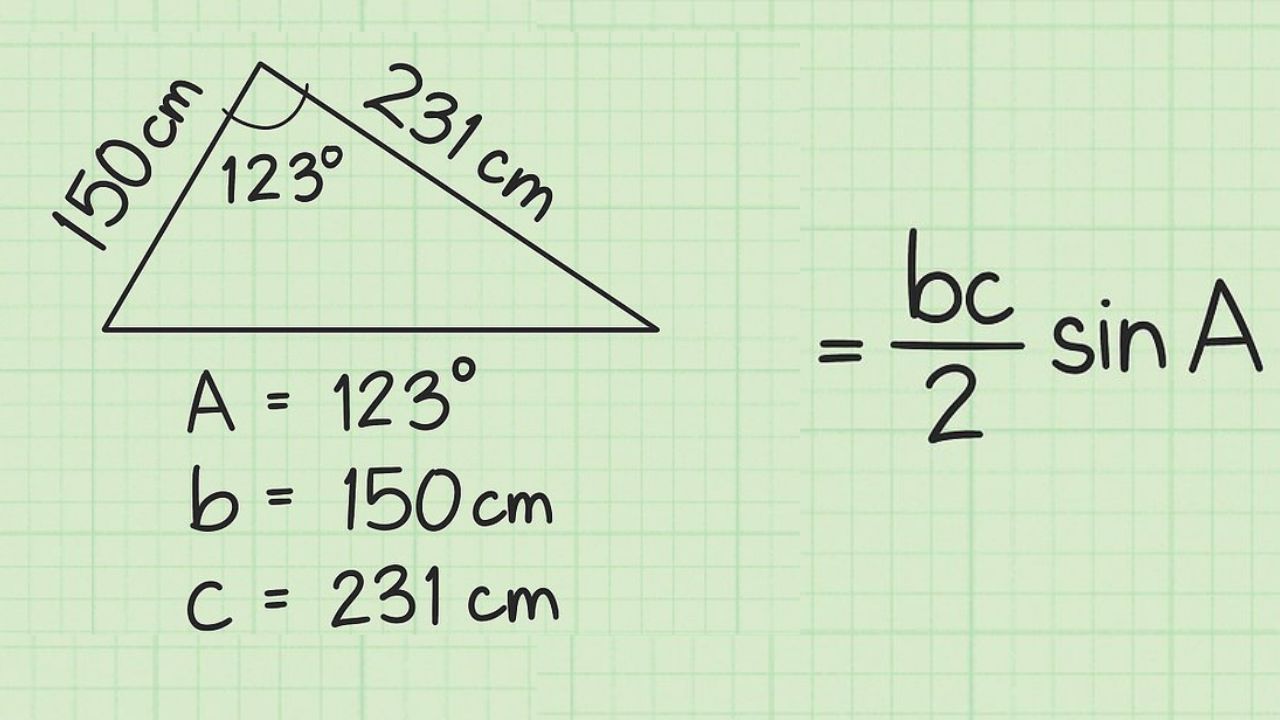
Bu yöntemi kullanarak sorunları çözmek oldukça kolay gibi görünse de, trigonometri İyi bir bilgiye sahip olmalısınız. Trigonometri kullanılarak çözülen bu tür üçgen alan problemleri, en zor sorular ayrıca formlar. Farklı denklemler söz konusu olduğunda formülleri doğru bir şekilde hatırlamak zor olacaktır.

Kaynak ve görseller: WIKIHOW