Üniversite öğrencisi değilseniz veya işinizde aktif olarak kullanıyorsanız lise geometri dersinde üçgenlerle karşılaşmış olabilirsiniz. Ülkemizde matematik ve geometri genellikle sevilmediğinden, bu derslerde gördüğümüz aslında üçgenler ve benzeri şekiller Hayatın birçok farklı alanında kendini gösterdiğini fark etmemiz kolay değil.
Elbette bu yazıda hayattaki üçgenlerden değil, geometrideki üçgenlerden bahsedeceğiz. Bazı üçgenler açı dereceleri ve kenar uzunlukları ile sabitlenmiştir. Bu üçgenlere özel üçgenler denir. Her birinin kendi değişmez kuralları ve bazı önemli özellikleri vardır. Gelin özel üçgenler ne Daha yakından bakalım ve her birinin önemli noktalarını görelim.
Özel Üçgenler nedir?

Açılarına göre özel üçgenler
- 30 – 60 – üçgen 90
- 30 – 30 – 120 üçgen
- 45 – 45 – üçgen 90
- 15 – 75 – 90 üçgen
30 – 60 – üçgen 90
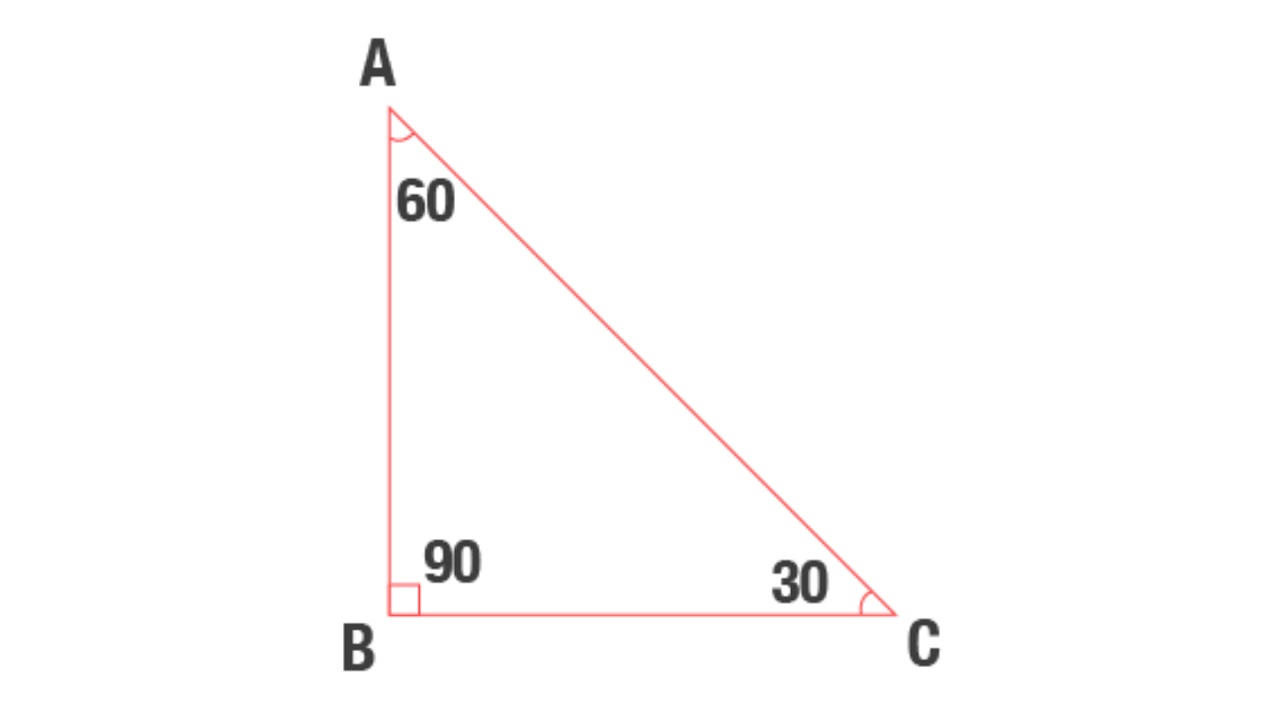
30 – 60 – 90 üçgeninde, üçgenin bir köşesinin açısı 30 derece, bir köşenin açısı 60 derece ve bir köşenin açısı 90 derecedir. 90 derecelik açının karşısındaki kenar hipotenüstür. Bu kenar, üçgenin en geniş açısına baktığı için üçgenin en uzun kenarıdır.
30 – 30 – 120 üçgen
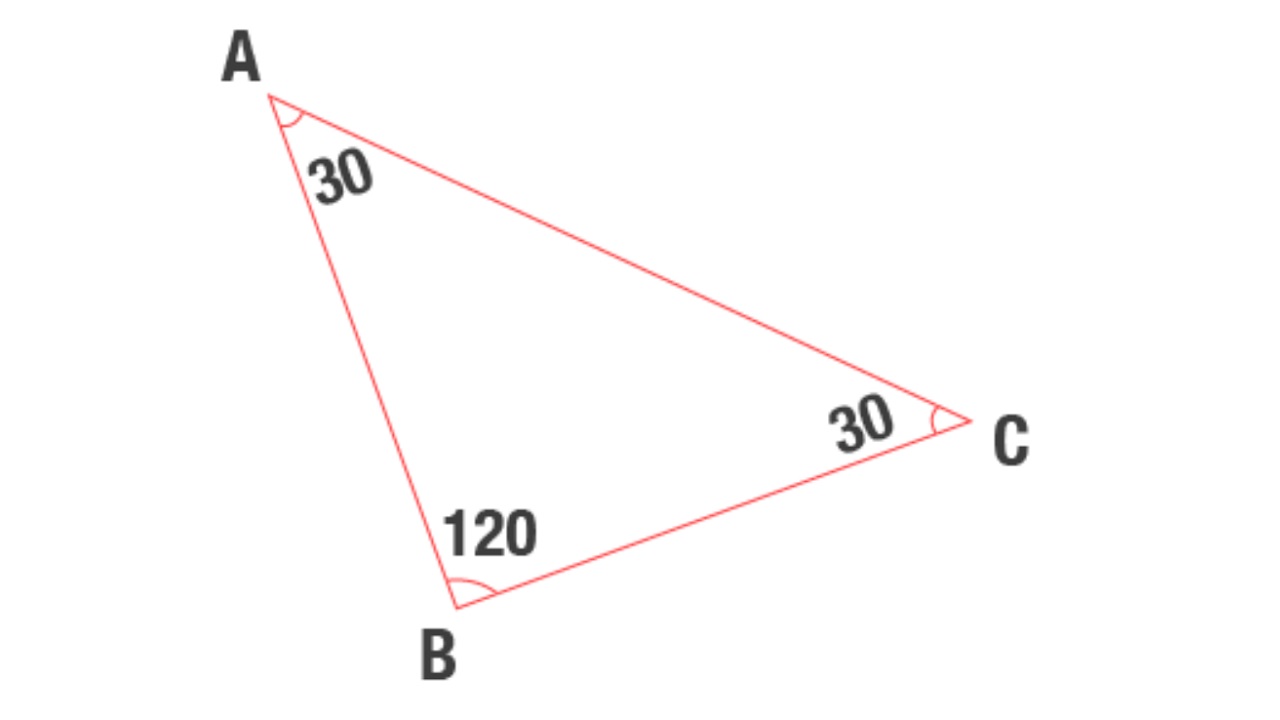
30 – 30 – 120 üçgende, üçgenin bir köşesinin açısı 30 derece, bir köşenin açısı 30 derece ve bir köşenin açısı 120 derecedir. 30-30-120 üçgeninde geniş açının karşısındaki kenarı bulmanın başka bir yolu daha vardır. Bu üçgende 30 derecelik köşelerin karşısındaki kenarlar için √3 değeri hesaplanır. Bu hesaplamadan elde edilen değer karşı kenardır.
45 – 45 – üçgen 90
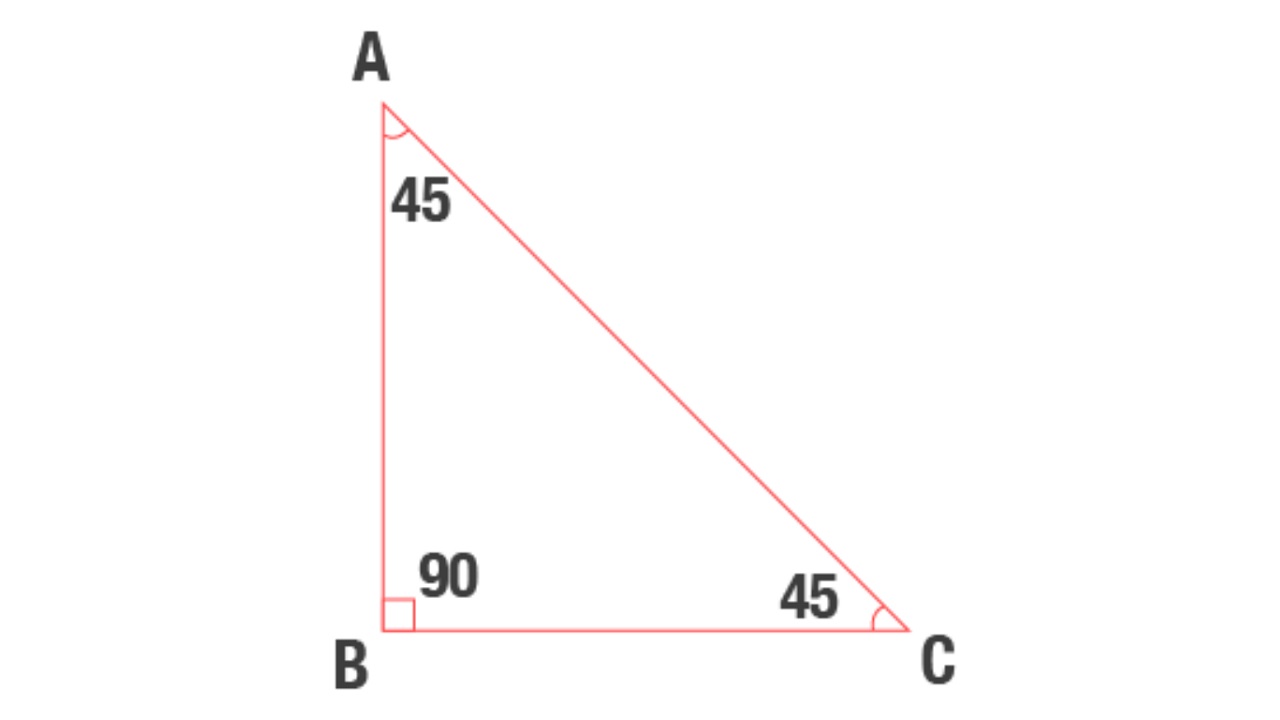
45 – 45 – 90 üçgeninde, üçgenin bir köşesinin açısı 45 derece, bir köşenin açısı 45 derece ve bir köşenin açısı 90 derecedir. 45 – 45 – 90 üçgeninde hipotenüsü bulmak için başka bir yöntem kullanılır.Bu üçgende 45 derecelik köşelerin karşısındaki kenarlar için √2 hesaplanır. Bu hesaplamadan elde edilen değer, bu hipotenüs. 45-45-90 üçgeni ikizkenar üçgendir.
15 – 75 – 90 üçgen
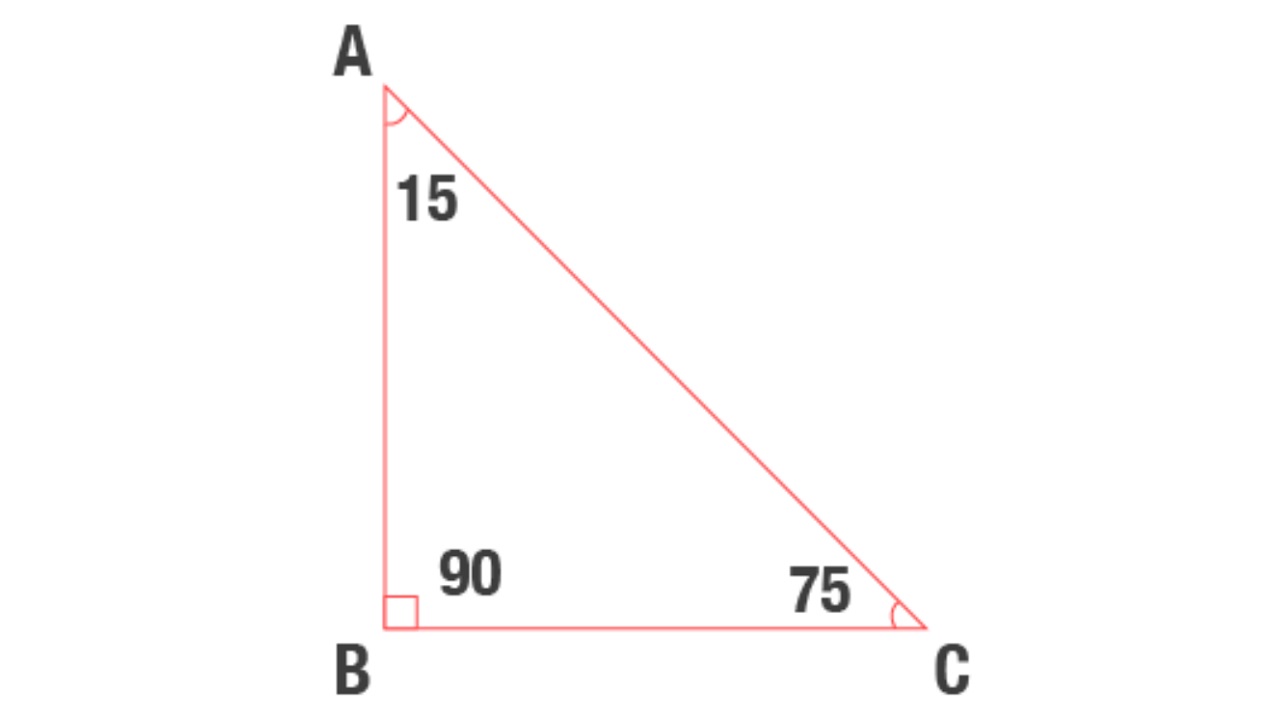
15 – 75 – 90 üçgeninde, üçgenin bir köşesinin açısı 15 derece, bir köşenin açısı 75 derece ve bir köşenin açısı 90 derecedir. 15 – 75 – 90 üçgeni hipotenüsü bulmak için farklı bir yöntem kullanır. Bu üçgende hipotenüs üçgenin yüksekliğinin dört katıdır. 15-75-90 üçgeni bir dar üçgendir.
Yanlardaki üçgenler
- 3 – 4 – 5 üçgen
- 8 – 15 – 17 üçgen
- 5 – 12 – 13 üçgen
- 7 – 24 – 25 üçgen
- ikizkenar üçgen
- Eşkenar üçgen
3 – 4 – 5 üçgen
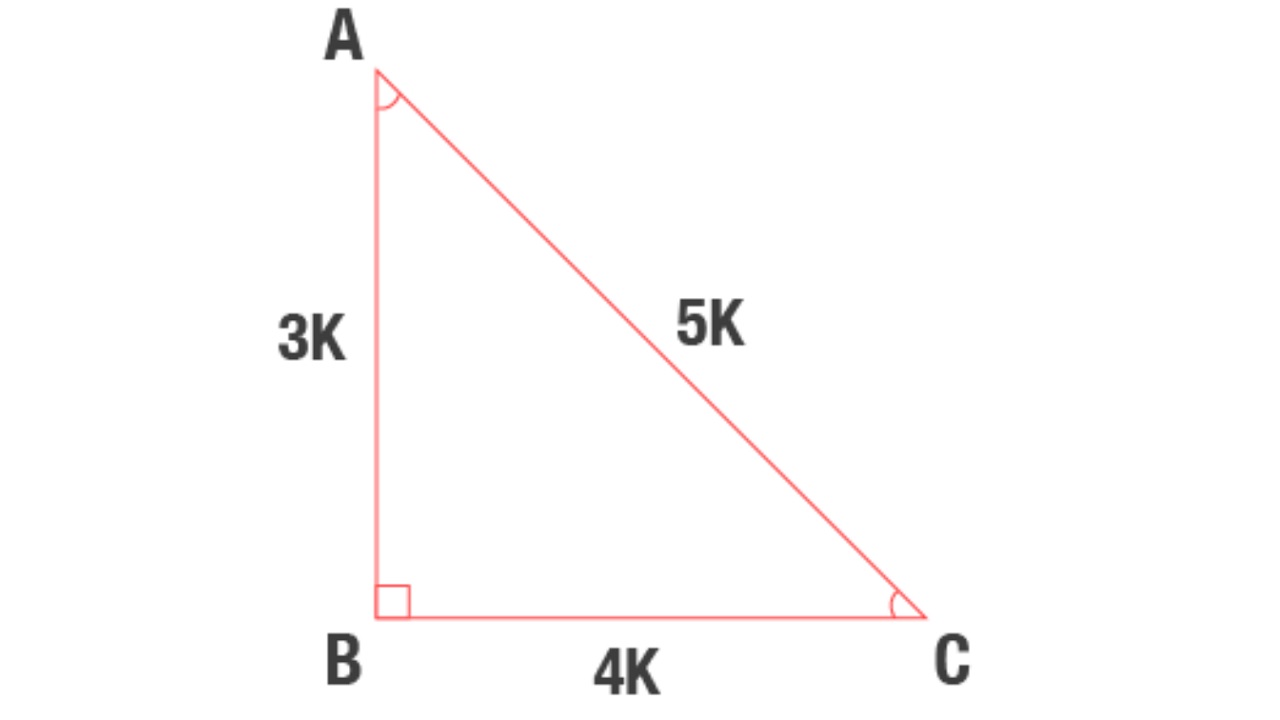
3 – 4 – 5 üçgeninde, üçgenin bir kenarının uzunluğu 3 ve 3’ün katıdır, bir kenarın uzunluğu 4 ve 4’ün katıdır ve bir kenarın uzunluğu 5’in katıdır ve 5. Üçgenin uzunluğunun uzunlukları ne olursa olsun, 3 – 4 – 5 her zaman bu sayıların bir katıdır. bir üçgendeki açılar 3 – 4 – 5; 36.87 derece, 53.13 derece ve 90 derece.
8 – 15 – 17 üçgen
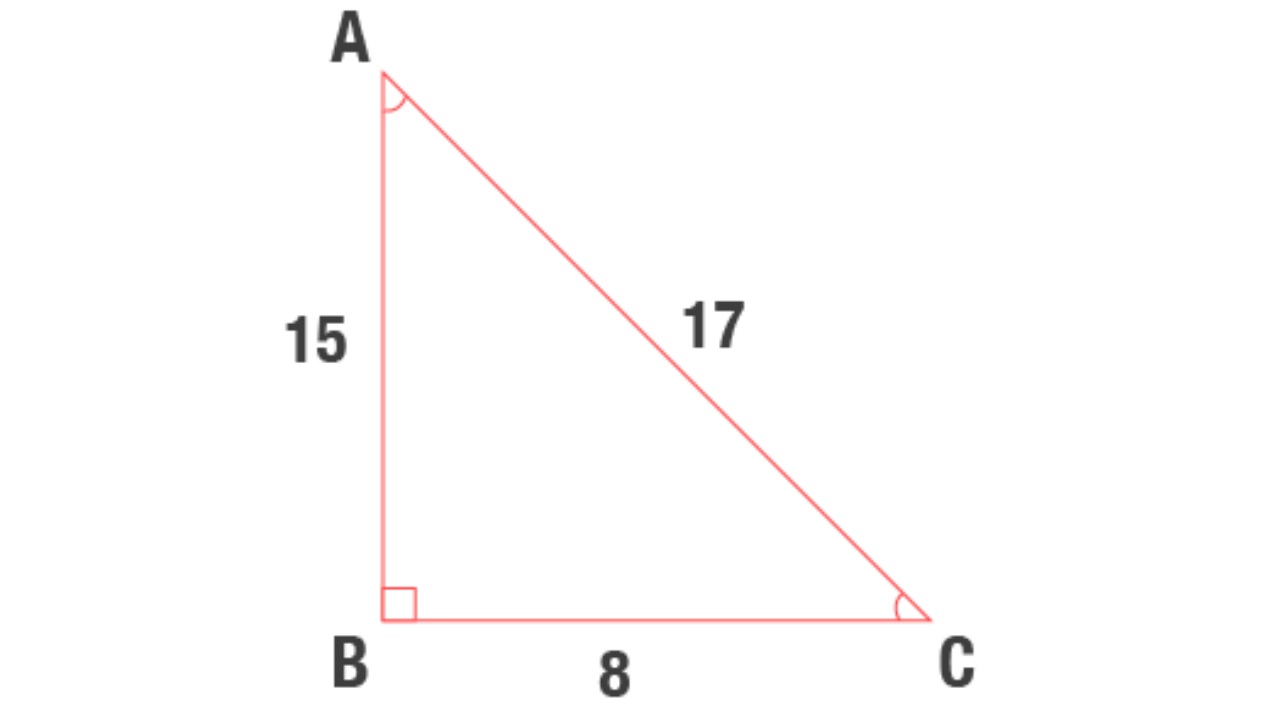
8 – 15 – 17 üçgeninde, üçgenin bir kenarının uzunluğu 8 ve 8’in katıdır, bir kenarın uzunluğu 15 ve 15’in katıdır ve bir kenarın uzunluğu 17’nin katıdır ve 17. Uzunluk ölçümleri ne olursa olsun, 8 – 15 – 17 üçgenindeki uzunluklar her zaman bu sayıların katlarıdır.
5 – 12 – 13 üçgen
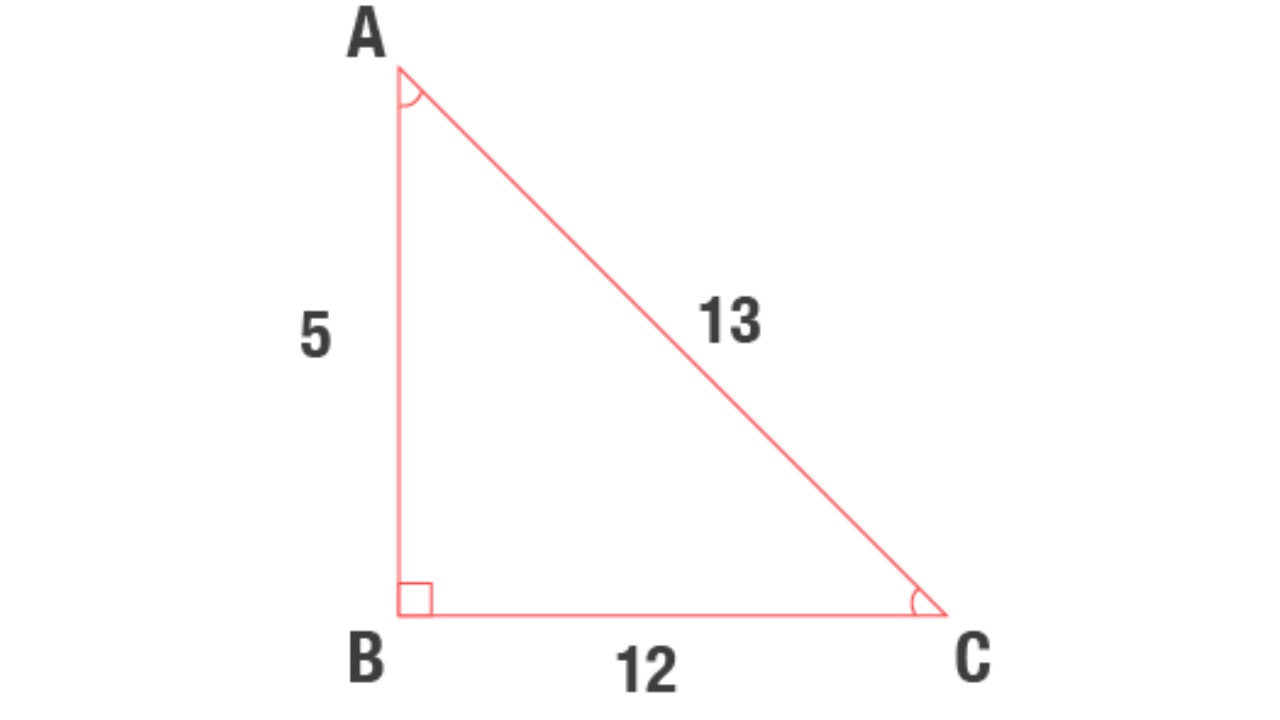
5 – 12 – 13 üçgen bir kenar uzunluğu 5 ve 5’in uzunluğu 12’nin katıdır, bir kenarın uzunluğu 12’nin katıdır ve bir kenarın uzunluğu 13 ve 13’ün katıdır. Uzunluk ölçümünden bağımsız olarak, bir üçgendeki uzunluklar 5 – 12 – 13 her zaman bu sayıların katlarıdır.
7 – 24 – 25 üçgen
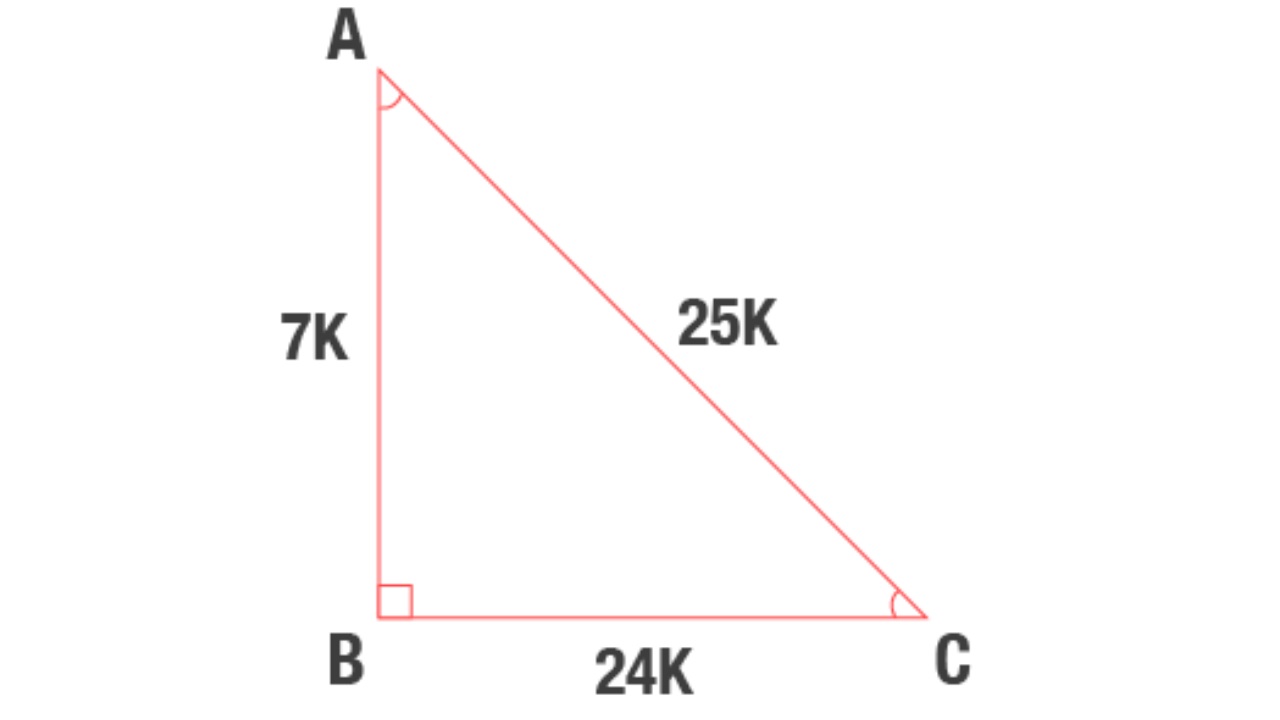
7 – 24 – 25 üçgeninde, üçgenin bir kenarının uzunluğu 7 ve 7’nin katıdır, bir kenarın uzunluğu 24 ve 24’ün katıdır ve bir kenarın uzunluğu 25’in katıdır ve 25. Uzunluğu ne olursa olsun 7-24-25 üçgeninde uzunluklar her zaman bu sayıların katlarıdır.
ikizkenar üçgen
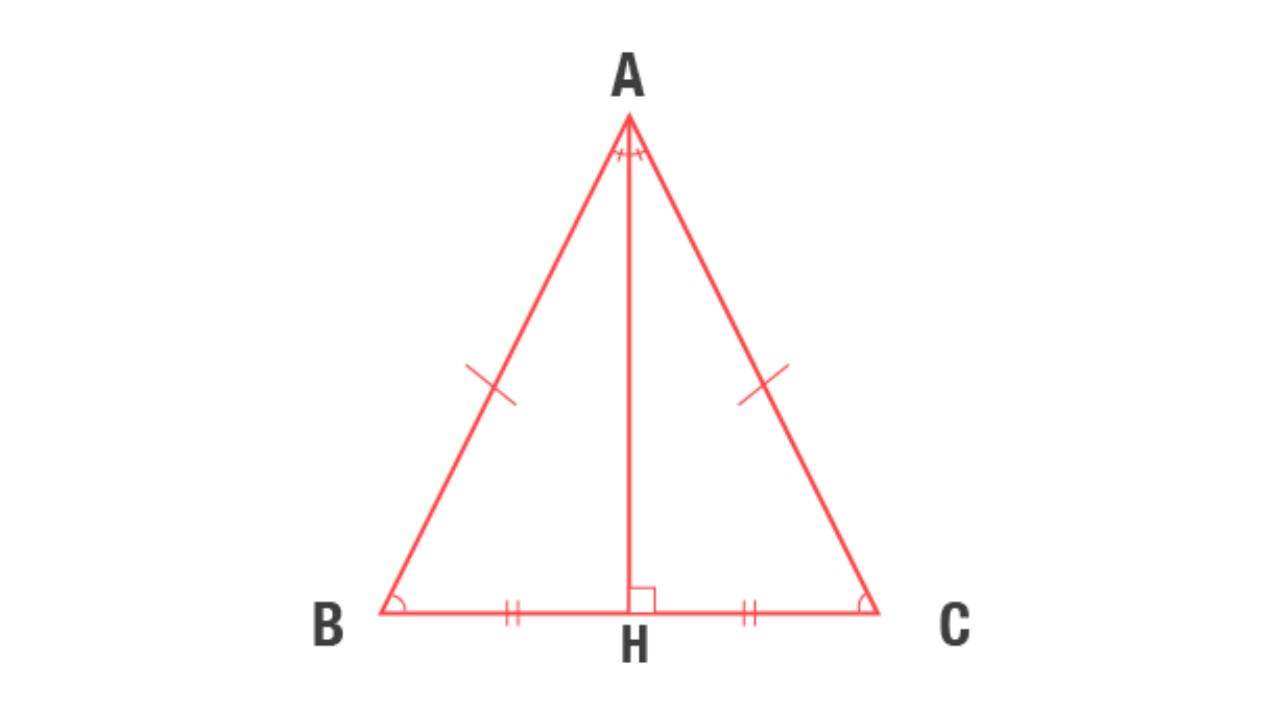
Bir üçgen alın ve hem ortayı hem de ortancayı iki eşit parçaya bölecek şekilde dikeyi indirin. Sonuçları hesaplarken görünen kenarlar eğer eşitlerse Elinizde bir ikizkenar üçgen var. Üçgeni tekrar alın ve tabandan iki tarafa iki paralel çizgi çizin. Bu paralellerin uzunluklarını toplayın. İşlem sonucunun bir kenar uzunluğuna eşit olduğunu göreceksiniz.
Eşkenar üçgen
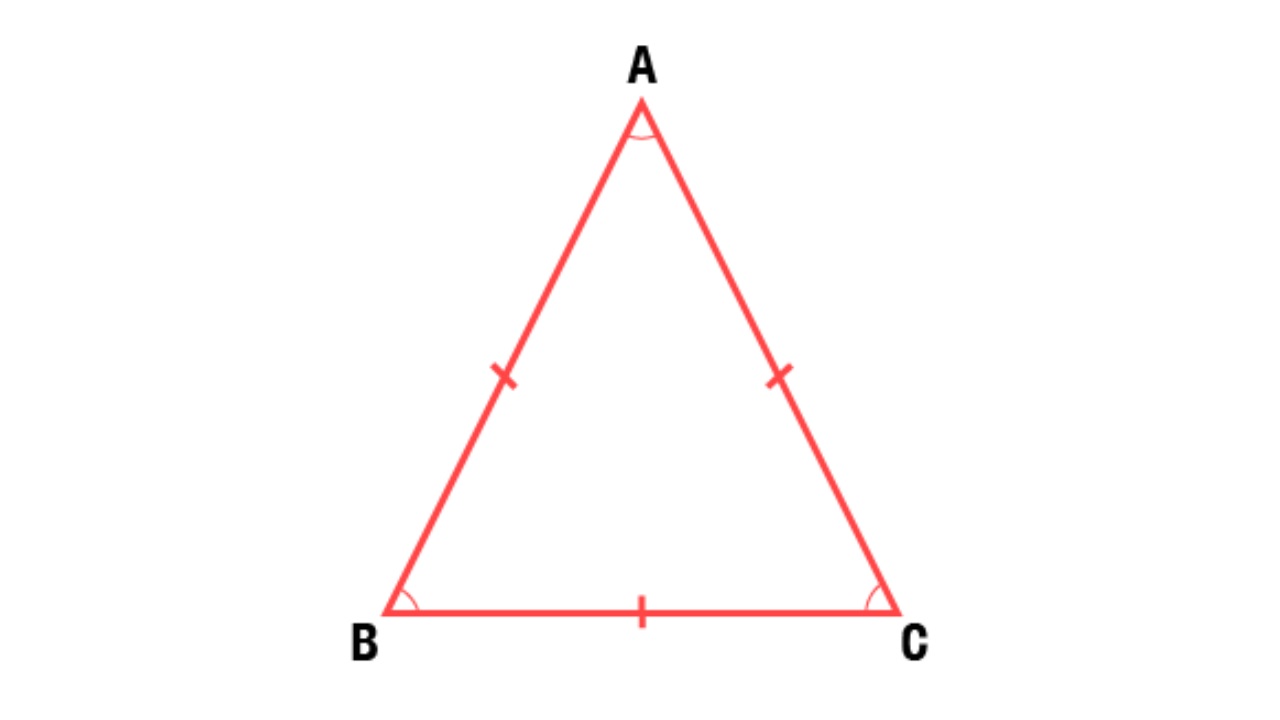
Bir üçgenin tüm kenarları eşit ise bu üçgene eşkenar üçgen denir. Eşkenar üçgenin bir köşesinden düz bir çizgide inen bir yükseklik oluşturduğunuzda, bu yükseklik hem medyanı hem de bisektörü oluşturur.
Üçgenler hakkında bilmeniz gerekenler:
Hepimizin hatırladığı gibi, bir üçgenin iç açıları toplamı 180 derecedir. Köşeleri A, B ve C olarak adlandırılır. ABC üçgenini düşündüğümüzde, BC köşelerine paralel bu üçgenin A noktasından geçen bir dik çizin ve BC çizgisinin açıları bu parçanın yarısını kaplayacaktır. Bir üçgenin herhangi bir dış açısını hesaplamak için, o dış açıya bitişik olmayan iki iç açıyı eklemeniz yeterlidir.
Yukarıda detaylandırdığımız özel üçgenler eşkenar üçgen, ikizkenar üçgen, eşkenar üçgen, dar üçgen, dik üçgen, geniş üçgen gibi farklı isimlere sahiptir. Üçgen hesaplamak için bazı oranlar vardır. Pisagor teoremi, kenar yöntemi, açı yöntemi, Heron yöntemi, kosinüs teoremi ve Öklid oranı gibi çeşitli isimlerle adlandırılırlar.
Bir köşe, bir kenar, bir iç açı, bir dış açı, bir derece, bir uzunluk gibi temel öğelere ek olarak, üçgenlerin bir açıortayı ve bir medyanı da vardır. iki farklı asistan mevcut. Üçgenlerin ortaya çıkardığı farklı açılara ve uzunluklara sahip geometrik şekilleri incelemek için birçok farklı teorem vardır. Aralarında en ünlüsü Ceva teoremi, Menelaus teoremi, Steward teoremi ve Carnot teoremidir.
En ünlü geometri nesnelerinden biridir ve yaşamın hemen her alanında bulunur. özel üçgenler nelerdir sorusuna cevap olarak bu özel üçgenlerin özelliklerinden ve genel olarak üçgenler hakkında bilmeniz gereken detaylardan bahsettik.





2 Comments
Leave a Reply